The hypot() Mystery

I was writing a section for the Code Reading followup volume, and wanted to demonstrate the pitfalls of using homebrewn mathematical functions instead of the library ones. As an example, I chose to compare the C library hypot(x, y) function, against sqrt(x * x, y * y). I created a plot of "unit in last place" (ulp) error values between the two functions, which demonstrated how the error increased for larger values of y.

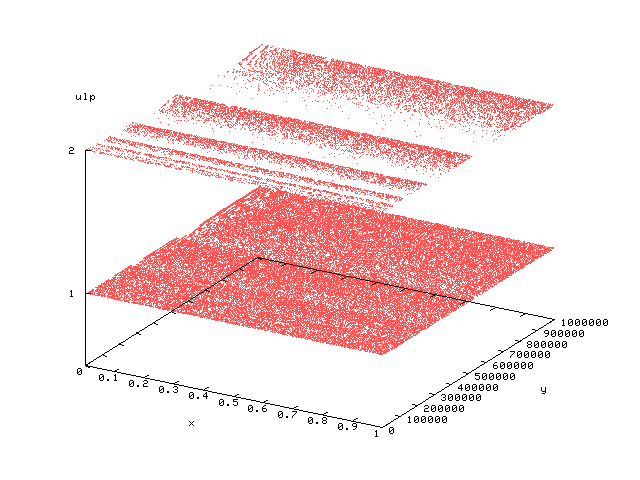However, I was feeling uneasy. The error distribution was not what I was expecting. First I thought the culrpit was the implementation of the ulp function. I was using David M. Gay's ulp implementation supplied with the FreeBSD gdtoa library, and was not sure how it behaved outside the library's domain. I combined it with a small test stub, and found that the values it returned were indeed correct.

The next step involved educating myself on the intricacies of mathematical function implementation on William Kahan's web page, and try some simple tests on hypot. The first test involved writing a test program to test hypot on arguments that formed Pythagorean triplets (Vasilis Capouleas advised me on the existence of formulas to derive them).

Amazingly, the function that returned a non-integer result was not the sqrt(x * x, y * y) function, but hypot(). The table at the end of this entry summarizes the wrong values for triplets derived from numbers up to 100. I was able to reproduce the errors with both Microsoft's Visual C compiler and the GNU C (Win32 mingw) compiler, both with, and without the "improve floating point consistency" switches (-Op and -ffloat-store). However, I was unable to reproduce the results on any non-Windows machine: Linux, and several versions of FreeBSD. Preplexed, I searched for the imports of the Windows executable files, and saw that they were importing hypot() from MSVCRT.DLL (version 7.0.2600.1106 - xpsp1.020828-1920). Mystery solved.

The C99 standard (Section 5.2.4.2.2) states that the accuracy of floating point functions is implementation-defined, so having hypot() return a 1 ulp error is allowed by the standard. Still, I find it surprising that with Sun's implementation, which guarantees a return value < 0.97 ulp, freely available since 1993 Microsoft is still distributing a less accurate implementation.

Indicative MSVCRT.DLL hypot() Errors

a	b	c	hypot(a, b)
99	20	101	100.99999999999999
45	108	117	116.99999999999999
165	52	173	173.00000000000003
153	104	185	185.00000000000003
221	60	229	229.00000000000003
57	176	185	184.99999999999997
171	140	221	220.99999999999997
209	120	241	240.99999999999997
21	220	221	221.00000000000003
63	216	225	225.00000000000003
357	76	365	365.00000000000006
399	40	401	401.00000000000006
69	260	269	268.99999999999994
299	180	349	348.99999999999994
391	120	409	409.00000000000006
483	44	485	485.00000000000006
425	168	457	456.99999999999994
81	360	369	368.99999999999994
189	340	389	389.00000000000006
459	220	509	508.99999999999994
567	144	585	584.99999999999989
675	52	677	677.00000000000011
261	380	461	461.00000000000006
319	360	481	480.99999999999994
783	56	785	785.00000000000011
31	480	481	481.00000000000006
93	476	485	484.99999999999994
899	60	901	901.00000000000011
231	520	569	568.99999999999989
891	180	909	908.99999999999989
665	432	793	793.00000000000011
1155	68	1157	1156.9999999999998
481	600	769	768.99999999999989
925	372	997	996.99999999999989
1147	204	1165	1164.9999999999998
585	648	873	873.00000000000011
741	580	941	940.99999999999989
1131	340	1181	1181.0000000000002
123	836	845	844.99999999999989
205	828	853	852.99999999999989
451	780	901	901.00000000000011
697	696	985	985.00000000000011
1107	476	1205	1205.0000000000002
1599	80	1601	1600.9999999999998
43	924	925	924.99999999999989
129	920	929	928.99999999999989
215	912	937	937.00000000000011
301	900	949	949.00000000000011
387	884	965	964.99999999999989
903	704	1145	1145.0000000000002
1419	380	1469	1469.0000000000002
1505	312	1537	1536.9999999999998
45	1012	1013	1013.0000000000001
1305	592	1433	1432.9999999999998
1395	532	1493	1492.9999999999998
1485	468	1557	1557.0000000000002
1575	400	1625	1624.9999999999998
1665	328	1697	1696.9999999999998
1935	88	1937	1937.0000000000002
141	1100	1109	1108.9999999999998
329	1080	1129	1129.0000000000002
1645	492	1717	1717.0000000000002
1739	420	1789	1788.9999999999998
1927	264	1945	1945.0000000000002
441	1160	1241	1241.0000000000002
1225	888	1513	1513.0000000000002
1911	440	1961	1961.0000000000002
2303	96	2305	2304.9999999999995
1377	936	1665	1665.0000000000002
1887	616	1985	1985.0000000000002
2499	100	2501	2501.0000000000005
689	1320	1489	1488.9999999999998
1325	1092	1717	1716.9999999999998
55	1512	1513	1512.9999999999998
825	1400	1625	1625.0000000000002
1265	1248	1777	1776.9999999999998
1375	1200	1825	1824.9999999999998
2145	752	2273	2272.9999999999995
2475	500	2525	2524.9999999999995
2585	408	2617	2617.0000000000005
2915	108	2917	2917.0000000000005
399	1600	1649	1648.9999999999998
513	1584	1665	1664.9999999999998
627	1564	1685	1685.0000000000002
855	1512	1737	1736.9999999999998
1425	1312	1937	1936.9999999999998
1539	1260	1989	1988.9999999999998
2793	424	2825	2825.0000000000005
3021	220	3029	3028.9999999999995
177	1736	1745	1745.0000000000002
767	1656	1825	1824.9999999999998
2183	1056	2425	2425.0000000000005
2891	540	2941	2941.0000000000005
3009	440	3041	3040.9999999999995
3127	336	3145	3144.9999999999995
3245	228	3253	3252.9999999999995
3363	116	3365	3365.0000000000005
549	1820	1901	1901.0000000000002
671	1800	1921	1921.0000000000002
1159	1680	2041	2040.9999999999998
2745	848	2873	2873.0000000000005
3233	456	3265	3265.0000000000005
3355	348	3373	3373.0000000000005
3477	236	3485	3485.0000000000005
3599	120	3601	3600.9999999999995
189	1980	1989	1989.0000000000002
315	1972	1997	1996.9999999999998
441	1960	2009	2008.9999999999998
567	1944	2025	2025.0000000000002
693	1924	2045	2044.9999999999998
2709	1060	2909	2908.9999999999995
3087	784	3185	3184.9999999999995
3213	684	3285	3285.0000000000005
3591	360	3609	3609.0000000000005
3843	124	3845	3845.0000000000005
195	2108	2117	2116.9999999999995
3315	812	3413	3413.0000000000005
3445	708	3517	3516.9999999999995
3965	252	3973	3972.9999999999995
469	2220	2269	2268.9999999999995
871	2160	2329	2328.9999999999995
1139	2100	2389	2389.0000000000005
2211	1700	2789	2789.0000000000005
2479	1560	2929	2928.9999999999995
2613	1484	3005	3004.9999999999995
3149	1140	3349	3349.0000000000005
3551	840	3649	3648.9999999999995
3953	504	3985	3985.0000000000005
4355	132	4357	4357.0000000000009
207	2376	2385	2385.0000000000005
621	2340	2421	2420.9999999999995
2553	1696	3065	3065.0000000000005
2691	1620	3141	3140.9999999999995
2967	1456	3305	3304.9999999999995
3519	1080	3681	3681.0000000000005
3657	976	3785	3785.0000000000005
3795	868	3893	3893.0000000000005
3933	756	4005	4004.9999999999995
497	2496	2545	2544.9999999999995
781	2460	2581	2581.0000000000005
1349	2340	2701	2701.0000000000005
3195	1508	3533	3533.0000000000005
3337	1416	3625	3624.9999999999995
3621	1220	3821	3820.9999999999995
3763	1116	3925	3924.9999999999995
4615	408	4633	4633.0000000000009
4757	276	4765	4765.0000000000009
73	2664	2665	2665.0000000000005
657	2624	2705	2704.9999999999995
803	2604	2725	2724.9999999999995
2409	2120	3209	3209.0000000000005
2555	2052	3277	3277.0000000000005
2993	1824	3505	3505.0000000000005
3285	1652	3677	3676.9999999999995
3869	1260	4069	4069.0000000000005
4599	680	4649	4648.9999999999991
1275	2668	2957	2957.0000000000005
1425	2632	2993	2992.9999999999995
3525	1708	3917	3917.0000000000005
3675	1612	4013	4013.0000000000005
385	2952	2977	2976.9999999999995
1617	2744	3185	3185.0000000000005
1771	2700	3229	3228.9999999999995
2387	2484	3445	3445.0000000000005
2695	2352	3577	3576.9999999999995
3157	2124	3805	3805.0000000000005
3311	2040	3889	3889.0000000000005
4081	1560	4369	4369.0000000000009
4543	1224	4705	4705.0000000000009
4697	1104	4825	4825.0000000000009
5621	300	5629	5629.0000000000009
869	3060	3181	3181.0000000000005
1027	3036	3205	3205.0000000000005
1501	2940	3301	3300.9999999999995
2133	2756	3485	3484.9999999999995
2923	2436	3805	3804.9999999999995
4977	1136	5105	5104.9999999999991
5609	600	5641	5641.0000000000009
567	3256	3305	3304.9999999999995
729	3240	3321	3320.9999999999995
1377	3136	3425	3424.9999999999995
1701	3060	3501	3501.0000000000005
1863	3016	3545	3544.9999999999995
2025	2968	3593	3593.0000000000005
4455	1768	4793	4793.0000000000009
5103	1296	5265	5264.9999999999991
6075	468	6093	6093.0000000000009
6237	316	6245	6244.9999999999991
747	3404	3485	3485.0000000000005
1909	3180	3709	3709.0000000000005
4897	1704	5185	5185.0000000000009
5063	1584	5305	5305.0000000000009
5893	924	5965	5965.0000000000009
6391	480	6409	6409.0000000000009
6557	324	6565	6564.9999999999991
6723	164	6725	6725.0000000000009
935	3552	3673	3672.9999999999995
1445	3468	3757	3756.9999999999995
2295	3248	3977	3976.9999999999995
3145	2928	4297	4297.0000000000009
3825	2600	4625	4625.0000000000009
5525	1500	5725	5725.0000000000009
5695	1368	5857	5856.9999999999991
6205	948	6277	6277.0000000000009
6715	492	6733	6733.0000000000009
87	3784	3785	3784.9999999999995
609	3760	3809	3808.9999999999995
957	3724	3845	3845.0000000000005
1131	3700	3869	3869.0000000000005
2001	3520	4049	4049.0000000000005
4263	2584	4985	4985.0000000000009
4437	2484	5085	5085.0000000000009
4785	2272	5297	5296.9999999999991
5307	1924	5645	5645.0000000000009
5655	1672	5897	5896.9999999999991
5829	1540	6029	6028.9999999999991
6351	1120	6449	6449.0000000000009
6699	820	6749	6749.0000000000009
6873	664	6905	6905.0000000000009
7047	504	7065	7065.0000000000009
7221	340	7229	7228.9999999999991
7395	172	7397	7397.0000000000009
89	3960	3961	3961.0000000000005
267	3956	3965	3964.9999999999995
445	3948	3973	3973.0000000000005
979	3900	4021	4021.0000000000005
3649	3120	4801	4800.9999999999991
4361	2760	5161	5161.0000000000009
4717	2556	5365	5365.0000000000009
5429	2100	5821	5820.9999999999991
5785	1848	6073	6073.0000000000009
6141	1580	6341	6340.9999999999991
6853	996	6925	6924.9999999999991
7209	680	7241	7241.0000000000009
7387	516	7405	7404.9999999999991
7565	348	7573	7573.0000000000009
7743	176	7745	7745.0000000000009
1001	4080	4201	4201.0000000000009
5369	2400	5881	5880.9999999999991
6097	1896	6385	6384.9999999999991
6825	1328	6953	6952.9999999999991
7553	696	7585	7585.0000000000009
8099	180	8101	8101.0000000000009
465	4312	4337	4336.9999999999991
4185	3312	5337	5336.9999999999991
4371	3220	5429	5429.0000000000009
4929	2920	5729	5728.9999999999991
6603	1804	6845	6844.9999999999991
7161	1360	7289	7288.9999999999991
7347	1204	7445	7444.9999999999991
7719	880	7769	7768.9999999999991
7905	712	7937	7937.0000000000009
8091	540	8109	8109.0000000000009
1045	4452	4573	4572.9999999999991
4275	3500	5525	5524.9999999999991
5035	3108	5917	5916.9999999999991
5225	3000	6025	6024.9999999999991
5605	2772	6253	6253.0000000000009
5985	2528	6497	6496.9999999999991
6365	2268	6757	6756.9999999999991
7125	1700	7325	7325.0000000000009
7315	1548	7477	7477.0000000000009
7695	1232	7793	7792.9999999999991
8075	900	8125	8125.0000000000009
1649	4560	4849	4849.0000000000009
2037	4484	4925	4924.9999999999991
4947	3404	6005	6004.9999999999991
5335	3192	6217	6217.0000000000009
5917	2844	6565	6565.0000000000009
6111	2720	6689	6689.0000000000009
6499	2460	6949	6949.0000000000009
6693	2324	7085	7085.0000000000009
7857	1424	7985	7985.0000000000009
99	4900	4901	4901.0000000000009
297	4896	4905	4905.0000000000009
2079	4680	5121	5120.9999999999991
3069	4420	5381	5380.9999999999991
4059	4060	5741	5741.0000000000009
4455	3888	5913	5912.9999999999991
5049	3600	6201	6201.0000000000009
6633	2656	7145	7145.0000000000009
7227	2236	7565	7564.9999999999991
7623	1936	7865	7864.9999999999991
8019	1620	8181	8180.9999999999991
9603	196	9605	9604.9999999999982

Comments   Toot! Tweet Share