blog dds: 2009-08-05 — How to Create a Self-Referential Tweet

Yesterday Mark Reid posted on Twitter a challenge: create a self-referential tweet (one that links to itself). He later clarified that the tweet should contain in its text its own identifier (the number after "/status/" bit should be its own URL). I decided to take up the challenge ("in order to learn a bit about the Twitter API" was my excuse), and a few hours later I won the game by posting the first self-referential tweet. Here is how I did it.

By looking through the URLs of a few tweets I realized that the identifier was increasing over time, so I wrote a script to rapidly post tweets with the appropriate identifier in them. The first version of the script was a failure, but it allowed me to collect a sequence of successive tweet identifiers. It turned out that about one to two hundred other tweets were being posted between each of my script's tweets, thus hardening the guess for the next tweet identifier. With the identifiers in a spreadsheet I could safely experiment with various strategies without the risk of getting locked out of Twitter due to rapid tweeting.

My first attempt was a Newton-Raphson style approximation. If delta is the identifier difference between two tweets and error is the difference between the guessed identifier and the next one, I let the next guess be

lastId + delta + error / 2

This formula rapidly converged toward a small error, but failed to hit the nail.

Another attempt took a second derivative delta2 as the difference between two delta values and had the next guess be

lastId + delta + delta2

This also failed to predict an id value for the identifiers I had collected.

At that point I decided to look at the distribution of the delta values.
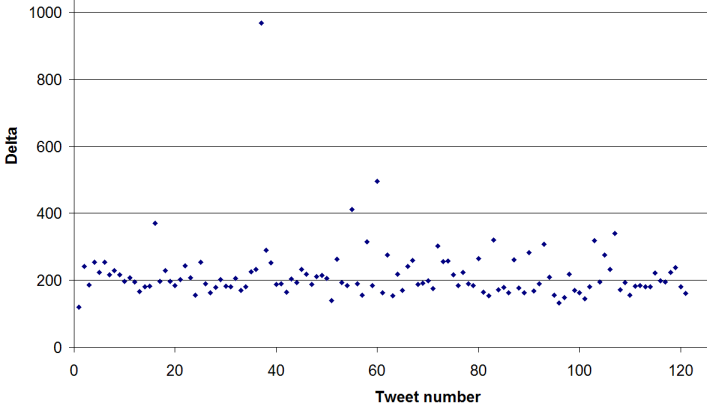
Twitter identifier differences
As you can see, there is a slight oscillation in the deltas, but this is not always discernable from one value to the next.

Therefore, my next try was simpler, rather than more complicated. I had guess be

lastId + delta

and hoped that raw power and chance would hit the correct result. Indeed, looking at the mean squared error of the three estimations I saw that the last and simplest formula had the lowest error value. This reminded me of Anatol Rapaport's simple tit-for-tat strategy which famously won in an iterated prisoner's dilemma tournament although it was the simplest of all programs entered.

I implemented the formula (as I had the initial one) in a simple shell script. Thankfully, I could easilly invoke Twitter's API just by executing curl with the appropriate arguments.

#!/bin/sh
#
# Create a self-referential tweet
# Diomidis Spinellis, August 2009
#

# Post a self-referential entry and return its id
getid()
{
	curl -s -u SelfRefer:$PASSWORD \
	-d "status=Self referential tweet http://twitter.com/SelfRefer/status/$selfid" \
	http://twitter.com/statuses/update.xml |
	sed -n '/<id>/{;s/.*<id>\([^<]*\)<\/id>.*/\1/p;q;}'
}

# Initial values
selfid=3125051561
delta=120
oldid=$selfid
error=0

while :
do
	id=`getid`
	delta=`expr $id - $oldid`
	oldid=$id
	selfid=`expr $id + $delta`

	error=`expr $id - $selfid`
	echo "id=$id error=$error delta=$delta selfid=$selfid"
	if [ $error -eq 0 ]
	then
		# Delete other entries
		while read id
		do
			curl -s -u SelfRefer:$PASSWORD --http-request DELETE \
			http://twitter.com/statuses/destroy/$id.xml >/dev/null
		done <todelete
		# Success; done
		exit 0
	fi
	echo $id >>todelete
done