|
http://www.spinellis.gr/pubs/jrnl/1999-MPE-GASA/html/gasa.html This is an HTML rendering of a working paper draft that led to a publication. The publication should always be cited in preference to this draft using the following reference:
|
| Diomidis D. Spinellis | Chrissoleon T. Papadopoulos |
| Department of Information and Communication Systems | Department of Business Administration |
| GR-832 00 Karlovassi | GR-821 00 Chios |
| University of the Aegean | University of the Aegean |
| Greece | Greece |
| dspin@aegean.gr | hpap@aegean.gr |
Keywords:
Simulated annealing, genetic algorithms, buffer allocation
AMS Classification:
90C15 Stochastic programming
The allocation of buffers between workstations is a major optimization problem faced by manufacturing systems designers. It has to do with devising an allocation plan for distributing a certain amount of buffer space among the intermediate buffers of a production line. It is a very complex task that must account for the random fluctuations in mean production rates of the individual workstations of the lines. To solve this problem there is a need for two different tools. The first is a tool that calculates the performance measure of the line which has to be optimized (e.g., the throughput or the mean work-in-process). This may be an evaluative method such as simulation, a decomposition method [1,2], or a traditional Markovian state model in conjunction with an exact numerical algorithm [3]. The second tool is a search (generative) method that tries to determine an optimal or near optimal value for the decision variables, which in our case are the buffer capacities of the intermediate buffer locations in the line. Examples of such methods are the classical search methods such as the well-known Hooke-Jeeves method, various heuristic methods, knowledge based methods, genetic algorithms, and simulated annealing.
Evaluative and generative (optimization) models can be combined in a `closed loop' configuration by using feedback from an evaluative model to modify the decision taken by the generative model. In such a configuration the evaluative model is used to obtain the value of the objective function for a set of inputs. The value of the objective function is then communicated to the generative model which uses it as an objective criterion in its search for an optimal solution. In the rest of this paper we will use the formalism S(G, E) to describe a closed loop system using the generative method G and the evaluative method E. The generative models that will be used in this paper are:
Furthermore, two evaluative models will be used:
An overview of the existing research in the area of evaluative and generative models of manufacturing systems can be found in two review papers [4,5] and a number of books [6,7,8,9,10,11].
Several researchers have studied the problem of optimizing buffer allocation to maximize the efficiency of a reliable production line [12,13,14]. Their results are based on comprehensive studies to characterize the optimal buffer allocation pattern. Authors have provided extensive numerical results for balanced lines with up to 6 stations and limited results for lines with up to 9 stations. However, few methods can handle this problem for large production lines, in a computationally efficient way. In this paper we compare two stochastic approaches suitable for large production lines, one based on genetic algorithms, and one based on simulated annealing. Details on how these methods can be applied to the problem can be found in the work by Bulgak et al. [15] which describes the application of genetic algorithms for the buffer allocation in asynchronous assembly systems and in our work [16] which describes a corresponding approach using simulated annealing. The implementation of both approaches in this paper works in close cooperation with a decomposition method [2].
Simulated annealing is an adaptation of the simulation of physical thermodynamic annealing principles [17] to the combinatorial optimization problems [18,19]. Similar to genetic algorithms and tabu search techniques [20] it follows the ``local improvement'' paradigm for harnessing the exponential complexity of the solution space. The algorithm is based on randomization techniques. An overview of algorithms based on such techniques can be found in the survey by Gupta et al. [21]. A complete presentation of the method and its applications is described by Van Laarhoven and Aarts [22] while a number of works present accessible algorithms for its implementation [23,24]. As a tool for operational research simulated annealing is presented by Eglese [25], while Koulamas et al. [26] provide a complete survey of simulated annealing applications to operations research problems.
Genetic algorithms [27,28,29] are global optimization techniques that avoid many of the shortcomings exhibited by local search techniques on difficult search spaces, such as the buffer allocation problem. Goldberg [30] describes a number of diverse genetic algorithm applications, while Karr [31] presents their use for modelling, design, and process control. Finally, Tompkins and Azadivar [32] use genetic algorithms for optimizing simulated systems.
This paper is organized as follows: Section 2 states the problem and the assumptions of the model and Section 3 describes the evaluation methodology and associated implementation decisions. In Section 4, we compare the numerical results obtained from the algorithms. Finally, Section 5 concludes the paper and suggests some future research directions.
In asynchronous production lines, each part enters the system from the first station, passes in order from all stations and the intermediate buffer locations, and exits the line from the last station. The flow of the parts works as follows: in case a station has completed its processing and the next buffer has space available, the processed part is passed on. Then, the station starts processing a new part that is taken from its input buffer. In case the buffer has no parts, the station remains empty until a new part is placed in the buffer. This type of line is subject to manufacturing blocking (or blocking after service) and starving.
The exponentiality of the processing times as well as the absolute reliability of the line's workstations are rather unrealistic assumptions. However, the service completion times can be exponential or can be approximated by an exponential distribution. The variability in completion times may be attributed to failures and repairs which implicitly exist in the problem at hand. Following this view, the proposed model may be applied to any unreliable production line under the exponentiality assumptions for the service completion times.
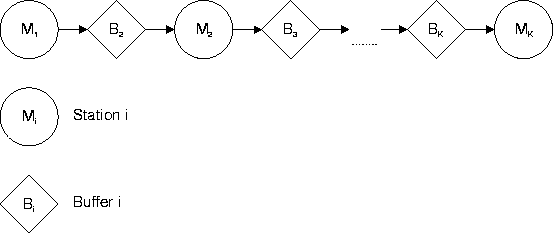
Figure 1 depicts a K-station line that has K-1 intermediate locations for buffers, labeled B2, B3, ¼, BK.

The basic performance measures in the analysis of production lines are the throughput (or mean production rate) and the average work-in-process (WIP) or equivalently the average production (sojourn) time.
The object of the present work is the buffering of asynchronous, reliable production lines with the assumptions given above. The objective is the maximization of the line's throughput, subject to a given total buffer space.
Find B = (B2,B3,¼,BK) so as toThe number of feasible allocations of N buffer slots among the K-1 intermediate buffer locations increases dramatically with N and K and is given by the formula:
subject to:
max
_
O
K(B) (1)
K
å
i = 2Bi = N
Bi ³ 0
Bi integer (i = 2,3,¼,K) (2) where:
- N is a fixed nonnegative integer, denoting the total buffer space available in the production line,
- B = (B2,B3,¼,BK) is the `buffer vector', i.e., a vector with elements the buffer capacities of the K-1 buffers, and
- [`O]K, denotes the throughput of the K-station line. This is a function of the mean service rates of the K stations, mi, (i = 1,2,¼,K), of the coefficients of variation, CVi, of the service times and the buffer capacities, Bi.
| (3) |
For this reason exhaustive search techniques are not practical for determining optimal configurations of production lines with a large number of stations or buffers.
We have evaluated different approaches for solving the optimal buffer allocation problem for large production lines, by performing the following steps:
In order to evaluate the applicability of the stochastic methods to the buffer allocation problem using comparable architectures we designed and implemented a system to calculate the optimum buffer configuration for a given reliable production line using a variety of algorithms [33]. The system takes as input:
Based on the above input, the system calculates the buffer allocations B = (B2,B3,¼,BK) for the maximal line throughput. Furthermore, the system is instrumented to provide as part of the solution the throughput of the suggested configuration, as well as the number of different configurations that were tried. The line throughput is used to evaluate the quality of the suggested configuration when compared with the throughput calculated by other methods. The number of different configurations tried, is used as an objective performance criterion, because the configuration evaluation step is the dominant execution time factor and the basic building block of all optimization methods. In addition, a special system configuration allows the creation of a file containing step-by-step snapshots of the algorithm progress. After obtaining the test results we wrote a number of scripts in the Perl programming language [34] that utilized the snapshot file to visualize and animate the dynamic behavior of the algorithms.
We ran a number of tests on both balanced and unbalanced lines and compared the stochastic method results against each other and against the results obtained by other methods. For short lines and limited buffer space a complete enumeration of all configurations provided an accurate measurement base to verify the stochastic algorithm results. For larger configurations we used a reduced enumeration in order to provide the comparative measure.
| (4) |
Our implementation of the simulated annealing algorithm for distributing N buffer space in a K-station line [16] follows the following steps:
An important characteristic of our implementation of the genetic algorithm concerns the representation of the solution. A good representation should ensure that the application of standard crossover recombination operators (where a new organism is composed from parts of two existing ones) would result in a valid new representation. Representing the line configuration as a vector B of buffers allocated across the line is not such a representation since given two buffer configurations (B1, B2) and recombining them as a new buffer B¢ at point c so that B¢0 ¼c ¬ B1, 0 ¼c and B¢c + 1 ¼K ¬ B2, c + 1 ¼K will not guarantee that åi = 1KB¢i = N i.e. that the resulting line configuration will be composed of N buffers. For this reason we devised an alternative, position-based, representation using a vector P of length equal to the number of buffers N. Every element of P can take values 0 ¼K representing the position of the given buffer slot within the production line. The two representations are equivalent; the vector P can be mapped to B as follows:
| (5) |
The implementation of genetic algorithms can be tuned using a number of different parameters. In our implementation we used the parameters that Grefenstette [35] derived using meta-search techniques namely:
The random floating point numbers 0 < R < 1 used for selecting energy differentials based on the annealing temperature R < exp([(-DE)/ T]), the crossover points, the mutation rates, and the selection of organisms are produced using the subtractive method algorithm [36]. Finally, the evaluative function that we used for calculating DE is based on the decomposition method [2].
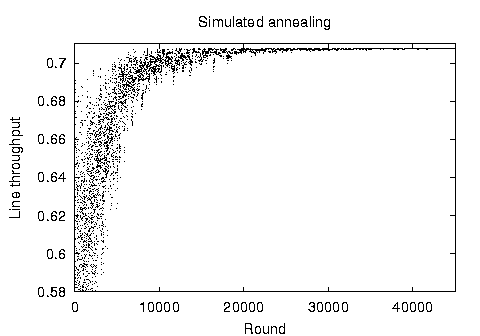
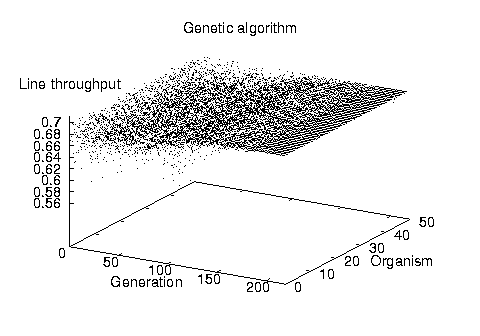
Before detailing the comparative results of our examination, it is interesting to visualize the operation of the two stochastic methods. Figure 2 depicts the runtime behavior of the two methods. Each point on the two scatter charts represents a given production line throughput value at a specific step of the algorithm. Both charts depict the calculation of the placement of 30 buffers in a balanced line of 10 stations. The simulated annealing algorithm optimizes a single solution in the specific example in 45.000 iterations. The solution's throughput value oscillates as both better and worse solutions are randomly selected at each iteration step. As can be seen on the chart, the oscillation width decreases following the algorithm's exponential cooling schedule and converges towards the optimal value.
The genetic algorithm is based on the implicit parallelism of the solutions represented by the initial population depicted on the chart's z-axis. Thus, in the specific example, it terminates with an optimal configuration after 250 generations. As the chart demonstrates the search starts with a wide spectrum of different solutions which are evaluated and evolve in parallel with non-optimal solutions gradually becoming extinct. Mutations and recombinations regenerate suboptimal solutions, but, due to the ``survival of the fittest'' organism selection strategy, their survival does not last for long.
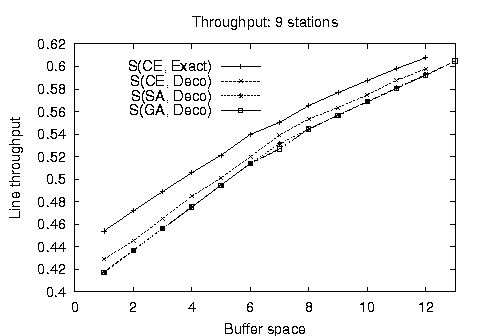
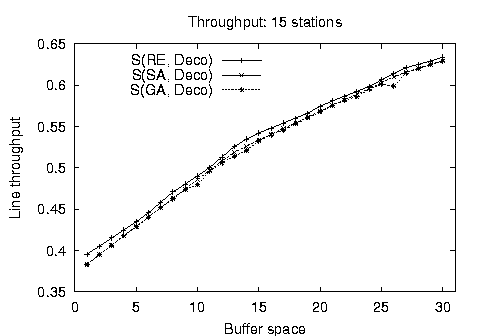
Our first comparison experiment concerned the algorithm operation on balanced lines for cases where exact solutions were known. In Figure 3 we present the optimum throughput configurations for balanced lines found using the stochastic methods against the throughput found using complete (for 9 stations) and reduced enumeration techniques. It is apparent that the stochastic algorithm results are almost identical and follow closely the results obtained by the other methods. Both methods are subject to the reduced evaluative accuracy of the decomposition method compared to the Markovian model.
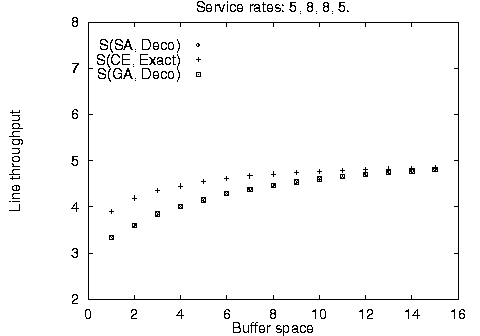
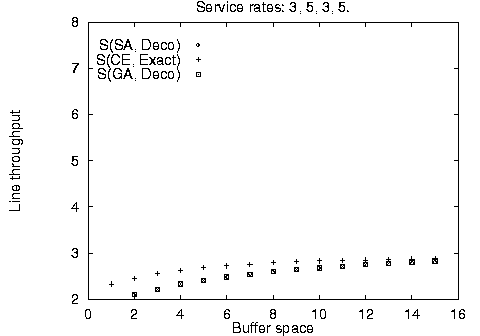
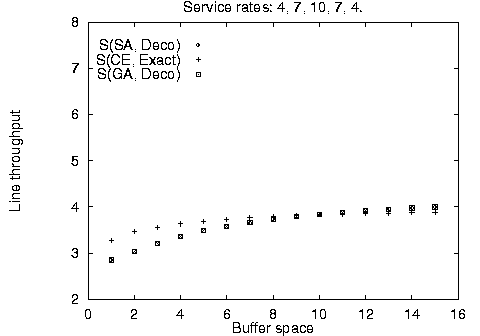
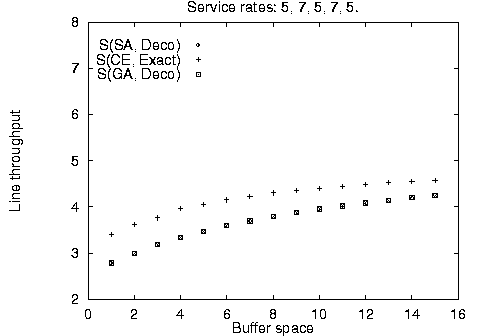
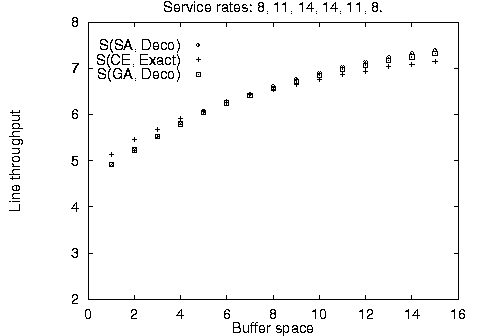
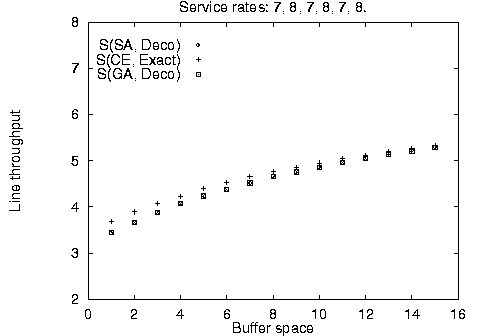
In addition to the balanced line evaluation, we compared the stochastic methods against unbalanced line enumeration using the Markovian evaluative procedure for a variety of line sizes, service time configurations, and available buffer space. The results are summarized in Figure 4. It is apparent, that the stochastic method configurations - although identical to each other - are not always optimal for limited available buffer space; however, they quickly converge towards the optimal configurations as buffer space increases. This difference can be accounted by the use of the fast decomposition evaluative procedure used in the stochastic algorithm implementation yielding approximate results against the use of the Markovian evaluative procedure for the enumeration method yielding exact results.
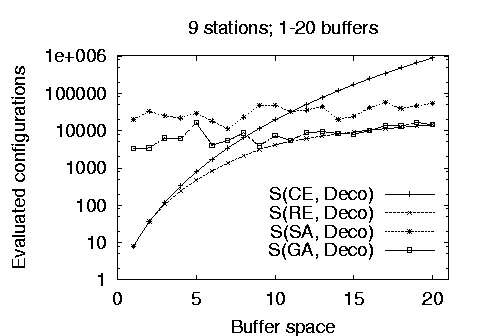
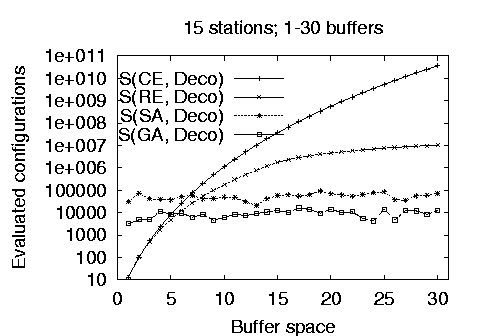
Our goal for using stochastic methods is to optimize large production line problems where the cost of other methods is prohibitively expensive. As an example the reduced enumeration method when run on a 15 station line with a buffer capacity of 30 units took more than 10 hours to complete on a 100MHz Pentium processor. As shown in Figure 5 the cost of the stochastic methods is higher than the cost of the full and reduced enumeration methods for small lines and buffer allocations. However, it quickly becomes competitive as the number of stations and the available buffer size increase. In addition, the performance of the genetic algorithm implementation is approximately an order of magnitude better than the simulated annealing implementation. Notice that - in contrast to the deterministic methods - the stochastic method cost does not increase together with the available buffer space and that it increases only linearly with the number of stations.
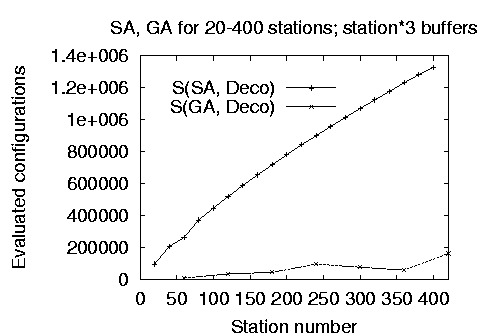
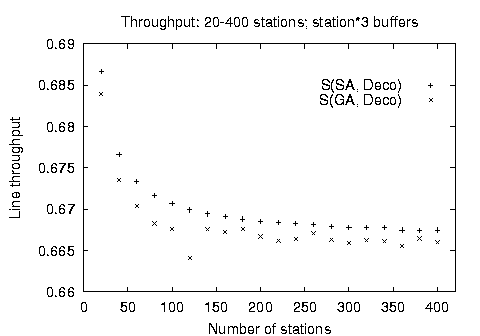
Finally, Figure 6 depicts the comparative performance and calculated throughput for the two stochastic methods when optimizing lines of up to 400 stations and 1200 buffers. The genetic algorithm implementation producing solutions with only 2.000.000 evaluations even for 400 station lines is clearly the performance winner. However, as depicted on the right hand chart, the throughput of the line configuration found by the genetic algorithm is consistently lower than the throughput of the line found by the simulated annealing method. The results we obtained could not be independently verified, because no other numerical results for the buffer allocation problem in large production lines can be found in the open literature.
Further investigation is needed in order to fully evaluate the potential of the two methods. The failure, in large production lines, of the genetic algorithm method to locate the optimal configuration found by the simulated annealing method is intriguing. It would be interesting to carefully examine the ``endgames'' of the two methods and find if and how the genetic algorithm implementation can be tweaked to evolve towards more optimal configurations. A dynamic re-adjustment of the algorithm's parameters (population size, crossover rate, mutation rate, etc.) forms one such possibility.
The annealing schedule and the genetic algorithm parameters that we used can clearly be optimized potentially increasing both methods' accuracy and performance. The use of heuristics in setting up the initial buffer configuration can decrease the number of steps needed for reaching the optimal. The differing relative strengths of the two stochastic approaches could also be combined in the form of a hybrid algorithm. Such an algorithm could capitalize on the rapid convergence exhibited by the genetic algorithms to quickly arrive at an acceptably efficient solution pruning away dead-ends. It could then pass the quickly derived buffer configuration to a simulated annealing algorithm which would use it as a starting point for obtaining an optimal solution.