Simulating Bandwidth-Limited Worms,
One Graph to Rule Them All?
Vasileios Vlachos, Eirini Kalliamvakou and
Diomidis Spinellis
Department of Management Science and Technology,
Athens University of Economics
and Business (AUEB),
Patission 76, GR-10434, Athens,
Greece
{vbill, ikaliam, dds}@aueb.gr
Abstract
Due to ethical and practical
limitations, simulations are the de facto approach to measure and
predict the propagation of malicious code on the Internet. A crucial part of
every simulation is the network graph that is used to perform the experiments.
Though recent evidence brought to light the nature of many technological and
socio-technical networks such as the web links, the physical connectivity of
the Internet and the e-mail correspondents, we argue that the interpretation of
these findings has to be strongly correlated with specific malware properties.
Furthermore, we question whether these graphs are accurate enough to model the
fastest spreading type of malicious activity, bandwidth-limited worms. Finally,
we propose some workarounds, by introducing a new Bandwidth-Aware Graphs Generation
Algorithm, in order to generate specially crafted network graphs for the
simulation of this type of malicious activity.
Keywords: malware,
networks, bandwidth-aware graphs
1. Introduction
The spread of
malicious software is definitely not a new threat, but only recently reached
epidemic proportions. Computer worms are, according to [Weaver et. Al. (2003)],
programs that self-propagate across a network exploiting security or policy
flaws in widely-used services. An emerging subcategory of them are the
bandwidth-limited worms, which mostly rely on the udp protocol to propagate in order to avoid the high-latency
issues that arise due to the three-way handshake of the tcp protocol [Cardwell et. Al. (2000)]. The most characteristic
examples are the Slammer [Moore et. Al. (2003)] and the Witty [Shannon & Moore (2004)] worms.
Identifying
and predicting the propagation patterns of rapid malcode clearly is not an easy
task. In vitro experiments with ‘live’ viral code raise numerous ethical
questions, because an unintended escape of a virus or a worm can cause severe
damages. Furthermore, to monitor the large scale effects that characterize the
propagation dynamics of various species of malicious software, a sustainable
number of systems is required which unfortunately exceeds the capabilities of
most laboratories.
An
alternative way to gather valuable information regarding the spread of a viral
agent is to collect empirical data during a malcode epidemic. This approach
faces two serious shortcomings. First, virus and worm epidemics don’t happen in
short, regular or predictable intervals. Second, even then, most of our
available resources and efforts are concentrated on the defence and the
recovery of the most critical digital infrastructures, leaving insufficient
time for theoretical studies.
Thus, simulating the
propagation of computer viruses and worms is the most widely accepted
methodology to measure and predict its consequences. One of the most important
factors of every network simulation, which is mostly overlooked, is the set of
characteristics of the graph that is utilized to represent a given network
topology. In this paper, we argue that the study of rapid malcode requires that
we take into account specific characteristics, such as connectivity, with
respect to the bandwidth of the infected hosts. Therefore, we question the
validity of the existing graphs that are frequently used to model the spread of
bandwidth limited worms, which utilize random scanning as their propagation
strategy.
The paper is organized as
follows. Section 2 presents the most commonly used graphs for the simulation of
rapid malcode. We provide examples of related research and give also the reasons
behind the choice of the specific graphs. In Section 3, we describe the related
work, whereas in Section 4 we discuss the accuracy of the specific models in
conjunction with some other efforts to address these problems. In Section 5, we
present some preliminary ideas to alleviate these issues without inducing
significant computational requirements and Section 6 concludes this paper.
2
Network Graph Models
Although graphs
have been widely used to study a variety of interesting theoretical problems,
only a small percentage of them are appropriate for network related problems in
general and even fewer are well suited to study the propagation dynamics of
rapid malcode. The most suitable topologies for this type of research are
homogenous graphs, random graphs and scale-free graphs.
2.1 Homogeneous Graphs
Most researchers
use homogeneous graphs for their simulations {[Berk et. Al. (2003)], [Kephart et. Al.
(1993)], [Kephart et. Al. (1999)], [Kephart et. Al. (1992)], [Chen et. Al
(2003)], [Zoo et. Al (2002)], [Staniford et. Al (2002)], [Staniford (2003)], [Scandariato
& Knight (2004)], [Zoo et. Al (2003)], [Leveille (2002)]}. In a homogeneous
graph (or complete graph) every node is connected with all the other nodes
resulting in a fully connected graph with N(N-1)/2 edges, where N
is the number of nodes. Homogeneous graphs are very popular among
epidemiologists studying the propagation of biological diseases and computer
epidemiologists as well because they offer significant advantages. Firstly, it
is very simple to construct them and secondly, most propagation patterns can be
calculated using mathematical epidemiological models. The rationale behind the
utilization of homogeneous graphs is that all ip
addresses are reachable from any system. Therefore, a worm can contact, connect
to and infect any other system regardless of its geographical proximity.
2.2 Random Graphs
For the last decades the common perception was that
almost all complex systems could be realistically modelled using random graphs.
The most widely accepted model is the one based on the Erdos-Rény (er) algorithm. The degree distribution
of an er graph obeys the
following Poisson distribution, given that N is sufficiently large .
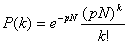 (1)
(1)
where P is the connection probability and k<N
the number of the neighboring nodes. Older research efforts {[Kephart et. Al (1993)], [Kephart &
White (1999)], [Kephart (1992)], [Zoo et. Al (2003)], [Leveille (2002)]} took
for granted that inherently complex systems, such as the Internet, should
follow a similar distribution and thus a random graph was a good approximation
for their experiments.
2.3
Scale-Free Graphs
Barabási
and Albert demonstrated that the creation of scale-free networks should include
two definitive characteristics: Incremental growth and preferential
connectivity. Furthermore,
Barabási and Albert [Barabási et. Al. (2003)] revealed that the
connectivity probability of the World Wide Web (www) and of most other complex social and technical systems
obey a power law distribution of the following type
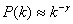 (2)
(2)
where 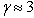 for the www. Their studies had great impact on
the virus research communities as other researchers discovered similar
structures in the www {[Kanovsky
& Mazor (2003)], [Adamic & Huberman (2000)], [Bornholdt & Ebel
(2001)]} and many other networks, such as the physical connectivity of the
Internet {[Faloutsos et. Al (1999)], [Medina et. Al (2000)]} or the network of
people exchanging e-mails [Ebel et. Al (2002)]. As the scale-free graphs became the de facto
standard to simulate the spread of worms {[Wang et. Al (2000)], [Leveille
(2002)], [Pastor-Satorras & Vespignani (2001)]} researchers have also tried
to incorporate bandwidth related issues. The work of [Weaver et. Al (2004)] and
[Wei et. Al (2005)] has made significant steps to address some of the related
issues.
for the www. Their studies had great impact on
the virus research communities as other researchers discovered similar
structures in the www {[Kanovsky
& Mazor (2003)], [Adamic & Huberman (2000)], [Bornholdt & Ebel
(2001)]} and many other networks, such as the physical connectivity of the
Internet {[Faloutsos et. Al (1999)], [Medina et. Al (2000)]} or the network of
people exchanging e-mails [Ebel et. Al (2002)]. As the scale-free graphs became the de facto
standard to simulate the spread of worms {[Wang et. Al (2000)], [Leveille
(2002)], [Pastor-Satorras & Vespignani (2001)]} researchers have also tried
to incorporate bandwidth related issues. The work of [Weaver et. Al (2004)] and
[Wei et. Al (2005)] has made significant steps to address some of the related
issues.
2.4 Other Topologies
In some older
experiments non-trivial graph topologies have been used to study the effects of
rapid malcode such as lattices {[Kephart et. Al (1993)], [Kephart (1992)]} and some
hierarchical tree-like structures [Wang et. Al (2000) ]. We believe that
these models have been abandoned today and are of limited use.
3 Discussion
All the above models have been extensively used in the
literature and have proven useful for the study of malware. We are not
confident though that their selection was made deliberately to depict specific
malware properties.
In particular, some researches
claim that a worm can reach any ip
address from any given one. Leaving aside the fact that many systems are behind
firewalls and use nat, or some
portions of the Internet address space are not routable at all, we have to
agree with this hypothesis. The interpretation of this assumption in most cases
is that any system contacts all the other systems during a simulation cycle and
has the opportunity to infect them, which according to common intuition is not
highly likely. In epidemiology, this phenomenon is known as homogeneous
mixing but it is not considered very realistic for large populations.
Other researchers, on the
other hand, argue that the scale-free graph models are the most appropriate.
While we also believe that this is the case, we feel that we have to more
thoroughly examine the foundations behind this hypothesis. In particular, there
are four major cases which need more elaboration.
3.1 Social relationships
The number of
friends each individual has follows a power low distribution [Barabási
(2003)]. Therefore, this social network is a scale-free graph. The practical
implications of this research in the context of computer virology can only be
attributed to the propagation of ‘ancient’ viruses via the now obsolete floppy
disks, which constitute no threat any longer.
3.2 World Wide Web
The www follows a power-law distribution
regarding the links that point from or to various web pages {[Kanovsky &
Mazor (2003)], [Adamic & Huberman (2000)], [Bornholdt & Ebel (2001)]}.
This evidence, while useful and important for many scientific fields, has
little to do with bandwidth-limited worms. In our context, we can make use of
this information only in some specific aspects of malcode such as some contagion
and web-based worms, like the Santy worm. Contagion worms that utilize
vulnerabilities in web-servers and web-browsers, such as the Nimda worm, to
stealthily propagate under the radar can best be described by these models but
their most important characteristic is that they can remain for long time
unnoticed. Unquestionably these worms are very dangerous but certainly do not
fall into the category of rapid malcode.
3.3 E-mail exchange
Studies showed that
networks of people exchanging e-mails form scale-free graphs [Ebel et. Al
(2002)]. This information is of strategic importance in the fight against mass
mailing worms. Many such worms have caused and still cause malware epidemics,
but hardly can they be considered as rapid malcode as they rely on clever
social engineering tactics and vulnerable e-mail clients to propagate.
3.4 Physical Connectivity of the
Internet
Theoretical and
empirical research confirms that the physical connectivity of the Internet
resembles a scale-free structure {[Faloutsos et. Al (1999)], [Medina et.al
(2000)]}. These studies examined the connectivity between bgp routers or Autonomous Systems and
concluded that it follows a power law distribution. Most of the simulations
that tend to use scale-free graphs follow closely the physical underlying
structure of the Internet. Though this assumption seems logical we have to
question its exact interpretation.
A
worm, in order to infect a target ip
address, has to traverse a number of intermediate routers. In general, the
intermediate routers are not in the position to alter, be infected by or modify
in any way the course of events once the transaction begins. Therefore, as
these routers do not play any active role in the evolution of an infection,
they can be omitted from an abstract connectivity model. Thus, this type of
communication between an attacking and a target node can be referred to as a direct
contact. Nonetheless, the importance of the scale-free nature of the Internet
is of great significance since it heavily affects its performance and
stability. While in that case the usefulness of the scale-free model is
evident, in the context of the malware propagation further investigation is
required to extract its exact implications.
4 Related Work
[Weaver et. Al
(2004)] made significant progress on the subject, but they encountered some
difficulties when they tried to combine topology maps of portions of the
Internet with bandwidth information. Their approach is valid, but since most of
the time these data are not available [Paxson & Floyd (1997)], synthetic
graphs have to be used instead. Another point that differentiates their work
from ours is that they use a single graph for modelling the connectivity of the
Internet with bandwidth information, which allows them to capture the
congestion effects that take place when a worm reaches its peak. We believe, on
the other hand, that the most important part, from an epidemiological point of
view of a malware epidemic, is its initial stages. The impact of the available
bandwidth strongly affects the propagation of a worm during the first steps of
the epidemic {[Staniford et. Al (2004)], [Weaver et. Al (2004)]}, because if it
reaches a critical mass of infected systems before countermeasures can be
deployed it is very hard to be contained.
[Ford et. Al (2005)]
take the bandwidth issue into consideration but they adapt bandwidth quotas to
the existing topologies they use. Thus, the basic underlying topology is
static, while each node has a different network capacity. In [Wei et. Al (2005)],
authors propose a very detailed simulation model which addresses
network-related issues down to the packet level. Their approach is nonetheless
valid, but requires excessive computational power as it is designed to work in
a distributed manner. In [Wagner et. Al (2003)], define various groups with
different connectivity and latency. Each node is then assigned to one of these
groups. While it is an interesting concept, they don’t provide enough
information regarding the instantiation of new contacts between the nodes of
these groups.
5 The Bandwidth-Aware Graph
Analytical models have certain restrictions, despite
the fact that scale well. Most importantly, these models cannot be easily
applied to large scale complex systems. As we discussed in a previous section,
the majority of the complex social and technical systems could best depicted as
random graphs or scale-free graphs. On the contrary, most of the times,
analytical models can only handle homogeneous graphs, which are not suitable
for the study of all the types of malicious activity. Most simulations are
computing-intensive making it necessary to introduce the right level of
abstraction in order to get meaningful results in reasonable time frames.
Combining the advantages as well as the shortcomings of the above graph models,
we propose some modifications that we find appropriate. We discuss also the
reasons these modifications are better suited for the study of rapid malware.
We believe that bandwidth
defines the connectivity of the graph. To be more specific, we argue that each
system can instantiate a connection and interact with any other system in the ip address space as long as it has the
available bandwidth to do so. (We leave aside the nat issue we mentioned earlier as it doesn’t significantly
change the landscape of a complex system, such as the Internet, nor can it be
addressed effectively by other means.) Therefore, every node in the graph
should be directly connected to any other. On the other hand, it is not
realistic to assume that each node will contact any other node during every
simulation cycle. To meet both of these requirements we consider the following
approach.
Given that a single graph
might not be sufficient to act as a realistic network topology regarding the
spread of malcode, we propose the use of multiple bandwidth-aware graphs as a
viable solution to increase the accuracy of the simulation. In particular, we
believe that each cycle of a worm-propagation simulation should be performed on
a different graph from a given graph set. All graphs which belong to the graph
set have very similar characteristics but they are not identical. Our model introduces
the bandwidth capacity (both in terms of uplink and downlink bandwidth) for
every node in a homogeneous graph. Thus, in every simulation cycle, a node will
be limited to contact randomly other nodes according to its predefined
bandwidth. In particular, a node i can contact a node j only if
the uplink capacity of node i
and the downlink capacity of node j
are greater than the size of the worm . To further
clarify the process of the creation of similar graphs we present analytically
the Bandwidth-Aware Graphs Generation Algorithm (bagga)
In the algorithm, N is
the set of all nodes in the graph, Up is the uplink capacity, D
is the downlink capacity and is the worm size.
The algorithm consists of two
parts:
A. Initialization
part
(1) Assign and
(2)
(3)
It should be noted that and
B. Main algorithm
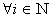
(1) if 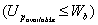 or
or 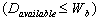 exit
exit
(2) if next i
(3) pick randomly 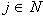
a. if 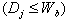 or (i connected to j)
repeat
or (i connected to j)
repeat
b. ,
c. ,
d. connect node i with node j
(4) repeat
We are aware of the existence
of various tools that generate graphs for network-related studies and at least
one of them is specially designed to construct topologies that are widely used
by computer epidemiologists [Vlachos et. Al (2005)]. Therefore, the
construction of a large number of graphs should be a trivial task.
We suggest the use of a unique
graph in each cycle of the simulation, after having built, in advance, a large
number of bandwidth-aware graphs with similar properties. Thus, while each node
eventually will have a direct contact with any other node in each time slot,
the number of its neighbours per time slot will be limited.
The above approximations will
be very important to researchers that cannot afford to perform packet level
simulations due to their complexity and the increased hardware requirements.
Furthermore, the bandwidth-aware graphs may also alleviate the shortage of
accurate graph topologies of the physical connectivity of the Internet,
considering that even in the cases where large organizations and isps have mapped significant portions
of the Internet, they are not willing to openly share this information.
Our aforementioned estimations
are largely based on our prior extended experience with graph generation. In
2005 we developed ngce, written
in Java (more than 5,000 lines of code, 15 Java classes, 150 lines of scripts).
The tool calculates the probability distribution, plots it, and provides
capabilities for building and analyzing various types of graphs. Furthermore, ngce’s output graph files are
compatible with the Pajek tool. For each different graph topology, a specific
plugin has been developed to implement the appropriate algorithm, making the
development of new algorithms as separate plugins extremely easy. We are
currently implementing the plugin for bagga
so as to provide further evaluation results.
A limitation of our model is
that it can handle only worms that employ random scanning as their propagation
strategy. Finally, to further improve the accuracy of this approach, each node
of the constructed graphs should follow the bandwidth distributions that have been
observed in related studies [Saroiu et. Al (2002)].
6 Conclusions
and Future Work
Simulations are, in general, the most prominent way to
explore the behaviour of complex systems. While the existing graph models are
satisfactory for the study of specific types of network issues such as routing,
resource preservation, and performance problems, the propagation of rapid
malcode requires a closer examination of the following aspects of the available
network models:
• Direct connectivity. All ip
addresses on the Internet are reachable from any ip address. The main difference between other network-related
simulations is that even if a worm requires many intermediate hops to reach its
target, these intermediate steps do not affect its propagation in any way.
• Node inequality. The decisive factor to estimate the number of
victims that each compromised system will manage to infect is its available
bandwidth. Therefore, treating each node of the Internet as equal is not the
most accurate approach. On the other hand, the available bandwidth of a node
has little to do with its geographical location or the physical connectivity
between the Autonomous Systems and bgp
routers.
The above reasons suggest the revaluation of the
existing graph models regarding their realism.
In our latest work [Vlachos et. Al (2005)], we presented the
ngce (Network Graphs for Computer
epidemiologists) tool which generates network graphs commonly used by computer
epidemiologists. We are in the process of implementing the proper plug-in for
the bagga in order to construct a
number of bandwidth-aware graphs and perform various simulations so as to
compare the results with the available empirical data.
Our intention is to
investigate the possibilities of creating realistic network topologies for the
study of the propagation of viral malcode having in mind that the access to
high-performance computers is limited and detailed Internet maps are not widely
available so as to perform detailed packet-level simulations and thus,
alternative ways to find meaningful abstractions are useful.
Acknowledgments
The work of
Vasileios Vlachos is funded under the Iraklitos fellowships for research of
Athens University of Economics and Business program and the European
Community's Sixth Framework Programme under the contract IST-2005-033331
“Software Quality Observatory for Open Source Software (SQO-OSS)'”.
References
Adamic, L., Huberman, B.
(2000) Power-law distribution of the
world wide web. Science 287(2115a)
Barabási, A., Bonabeau,
E. (2003) Scale-free networks.
Scientific American, pp. 60–69
Barabási, A.L. (2003) Linked. Penguin Group, printed in the
USA
Berk, V., Bakos, G., Morris,
R. (2003) Designing a framework for
active worm detection on global networks. In: Proceedings of the IEEE
International Workshop on Information Assurance, Darmstad, Germany
Bornholdt, S., Ebel, H. (2001)
World wide web scaling exponent from
simon’s 1955 model. Physical Review E 64 0345104 (R)–1 0345104–4
Cardwell, N., Savage, S.,
Anderson, T. (2000) Modeling TCP latency.
In: INFOCOM (3), pp. 1742–1751
Chen, Z., Gao, L., Kwiat, K.
(2003) Modeling the spread of active
worms. In: Proceedings of the IEEE Infocom. San Francisco, USA.
Clair-Ford, S., Ould-Khaoua,
M., Mackenzie, L. (2005) The impact of
network bandwidth on worm propagation. 21st UK Performance Engineering
Workshop CS-TR-916, School of Computing Science, University of Newcastle upon
Tyne, Claremont Tower, Claremont Road, Newcastle upon Tyne, NE1 7RU, UK
Ebel, H., Mielsch, L.,
Bornloldt, S. (2002) Scale-free topology
of e-mail networks. Physical Review E 66(035103(R))
Faloutsos, M., Faloutsos, P.,
Faloutsos, C. (1999) On power-law
relationships of the internet topology. In: Proceedings of ACM SIGCOMM,
Cambridge, MA, USA pp. 251–262
Kanovsky, I., Mazor, S. (2003)
Models of web-like€ graphs: Integrated
approach. In: Proceedings of the 7th World Multiconference on Systematics,
Cybernetics and Informatics (SCI 2003), Orlando, Florida, USA pp. 278–283
Kephart, J., Chess, D., White,
S. (1993) Computers and epidemiology.
IEEE Spectrum 30(20)
Kephart, J., White, S. (1999) Measuring and modeling computer virus
prevalence. In: Proceedings of the 1999 IEEE Computer Society Symposium on
Research in Security and Privacy, Oakland, California, pp. 2–14
Kephart, J. (1992) How topology affects population dynamics.
In: Proceedings of Artificial Life 3, New Mexico,USA
Leveille, J. (2002) Epidemic spreading in technological networks.
Hpl-2002-287, School of Cognitive and Computing Sciences, University of Sussex
at Brighton, Bristol
Medina, A., Matta, I., Byers,
J. (2000) On the origin of power laws in internet topologies. ACM Computer Communication
Review 30(2), pp. 160–163
Moore, D., Paxson, V., Savage,
S., Shannon, C., Staniford, S., Weaver, N. (2003) Inside the slammer worm. IEEE Security & Privacy, pp. 33–39
Pastor-Satorras, R.,
Vespignani, A. (2001) Epidemic spreading
in scale-free networks. Physical Review Letters 86, pp. 3200–3203
Paxson, V., Floyd, S. (1997) Why we don’t know how to simulate the
internet. In: Proceedings of the Winder Communication Conference.
Saroiu, S., Gummadi, P.,
Gribble, S. (2002) A measurement study of
peer-to-peer file sharing systems. In: Proceedings of Multimedia Computing
and Networking 2002 (MMCN’02).
Scandariato, R., Knight, J.
(2004) An automated defense system to
counter internet worms. Submitted to SRPS 2004, 23rd Symposium on Reliable
Distributed Systems, Florianapolis, Brazil.
Shannon, C., Moore, D. (2004) The spread of the witty worm. IEEE
Security & Privacy 2(4), pp. 46–50
Staniford, S., Moore, D.,
Paxson, V., Weaver, N. (2004) The top
speed of flash worms. In: WORM ’04: Proceedings of the 2004 ACM workshop on
Rapid malcode, New York, NY, USA, ACM Press, pp. 33–42
Staniford, S., Paxson, V.,
Weaver, N. (2002) How to 0wn the internet
in your spare time. In: Proceedings of the 11th USENIX Security Symposium,
pp. 149–167
Staniford, S. (2003) Containment of scanning worms in enterprise
networks. Journal of Computer Security
Vlachos, V., Vouzi, V., Chatziantoniou,
D., Spinellis., D. (2005) NGCE: Network
Graphs for Computer Epidemiologists. In Bozanis, P., Houstis, E.N., eds.:
In Advances in Informatics: 10th Panhellenic Conference on Informatics, PCI
2005, Lecture Notes in Computer Science 3746, Springer-Verlag pp. 672–683
Wagner, A., Dübendorfer,
T., Plattner, B., Hiestand, R. (2003) Experiences
with worm propagation simulations. In: In ACM Workshop on Rapid Malcode
(WORM).
Wang, C., Knight, J., Elder,
M. (2000) On computer viral infection and
the effect of immunization. In: Proceedings of the 16th Annual Computer Security
Applications Conference (ACSAC),New Orleans, Louisiana, USA, pp. 246–256
Weaver, N., Hamadeh, I.,
Kesidis, G., Paxson, V. (2004) Preliminary
results using scale-down to explore worm dynamics. In: ACM WORM,
Washington, DC
Weaver, N., Paxson, V., Staniford,
S., Cunningham, R. (2003) A taxonomy of
computer worms. In: First Workshop on Rapid Malcode (WORM).
Weaver, N., Paxson, V.,
Staniford, S. (2004) A worst-case worm.
In: Proceedings of the Third Annual Workshop on Economics and Information
Security (WEIS04)
Wei, S., Mirkovic, J., Swany,
M. (2005) Distributed worm simulation
with a realistic internet model. In: Proceedings of the 2005 Workshop on
Principles of Advanced and Distributed Simulation
Zou, C., Gao, L., Gong, W.,
Towsley, D. (2003) Monitoring and early
warning for internet worms. In: Proceedings of the 10th ACM Conference on
Computer and Communication Security, Washington DC, USA
Zou, C., Gong, W., Towsley, D.
(2002) Code red worm propagation modeling
and analysis. In: Proceedings of the 9th ACM Conference on Computer and
Communication Security (CCS), Washington DC, USA
Zou, C., Towsley, D., Gong, W.
(2003) Email virus propagation modeling
and analysis. Technical report, Umass ECE TR-03-CSE-04
