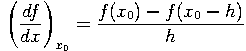
για μια αρκετά μικρή τιμή του h.
Παράδειγμα:
program maptest;
{$F+}
type
realmap = function(x : real) : real;
function map2(f : realmap; n : real) : real;
begin
map2 := f(f(n))
end;
function double(x : real) : real;
begin
double := x * 2
end;
begin
writeln(map2(double, 1))
end.
Το πρόγραμμα θα υπολογίσει την τιμή double(double(1)) και θα τυπώσει 4.
Για παράδειγμα με βάση τη διαδικασία map και αντίστοιχη συνάρτηση f μπορούμε εύκολα να δημιουργήσουμε από έναν πίνακα v έναν νέο πίνακα v' του οποίου τα στοιχεία να είναι διπλάσια κάθε στοιχείου του v:
program Map;
{$F+}
const
maxindex = 10;
type
realmap = function(x : real) : real;
mylist = array [1..maxindex] of real;
var
i : integer
l1, l2 : mylist;
procedure map(f : realmap; v : mylist; var vnew : mylist);
var
i : integer;
begin
for i := 1 to maxindex do
vnew[i] := f(v[i])
end;
function double(x : real) : real;
begin
double := x * 2
end;
begin
for i := 1 to maxindex do
readln(l1[i]);
map(double, l1, l2);
for i := 1 to maxindex do
writeln(l2[i]);
end.
σ1, σ2, σ3 ...τότε η νέα σειρά θα είναι:
f(...,f(σ3, f(σ2, f(σ1, α))))...
Για παράδειγμα με βάση τη συνάρτηση fold και αντίστοιχη συνάρτηση f μπορούμε εύκολα να βρούμε το άθροισμα των στοιχείων ενός πίνακα:
program TestFold;
{$F+}
const
maxindex = 10;
type
realmap = function(x : real; y : real) : real;
mylist = array [1..maxindex] of real;
var
i : integer;
l : mylist;
function fold(f : realmap; a : real; v : mylist) : real;
var
i : integer;
result : real;
begin
result := a;
for i := 1 to maxindex do
result := f(v[i], result);
fold := result;
end;
function sum(x : real; y : real) : real;
begin
sum := x + y
end;
begin
for i := 1 to maxindex do
readln(l[i]);
writeln(fold(sum, 0, l))
end.
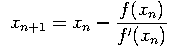
Η εύρεση της παραγώγου f' της f για μια τιμή x μπορεί και αυτή
να υπολογιστεί αριθμητικά ως:
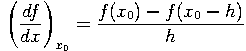
για μια αρκετά μικρή τιμή του h.
Το παρακάτω πρόγραμμα βρίσκει αριθμητικά μια ρίζα (1.4142135624) της εξίσωσης x^2 - 2 = 0.
program NewtonRaphsonExample;
{$F+}
const
Epsilon = 1e-8; {Αρκετά μικρή τιμή}
type
realfun = function(x : real) : real;
{Εύρεση παραγώγου της f για την τιμή x}
function DerivativeValue(f : realfun; x : real) : real;
begin
DerivativeValue := (f(x + epsilon) - f(x)) / epsilon
end;
{Εύρεση ρίζας της f για αρχική πιθανή τιμή x}
function NewtonRaphson(f : realfun; x1 : real) : real;
var
x0 : real;
begin
repeat
x0 := x1;
x1 := x0 - f(x0) / DerivativeValue(f, x0)
until abs(x1 - x0) < epsilon;
NewtonRaphson := x1
end;
{Εξίσωση - παράδειγμα (χ^2 - 2 = 0)}
function Example(x : real) : real;
begin
Example := sqr(x) - 2
end;
begin
writeln(NewtonRaphson(Example, 12))
end.

Function Integrate(f : realfun; a, b : real) : real;
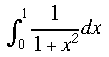
Ο υπολογισμός του ολοκληρώματος να γίνει σε ξεχωριστή συνάρτηση με παραμέτρους τη συνάρτηση για την οποία θα υπολογιστεί το ολοκλήρωμα, καθώς και τα άνω και κάτω όρια, α και β.